Chapter 10 --- The velocity of the electromagnetic field

Chapter
10

The velocity of the
electromagnetic field

As we know, the velocity , the mass m, and the momentum has the follows relationship:

(10.1)

Let us make the assumption that the above relationship is also valid within the electromagnetic field. As we know for the electromagnetic field, the momentum density is:

(10.2)

Per our assumption, the mass origin is from the electromagnetic field energy, so the mass density inside the electromagnetic field is:

(10.3)

In which u is the electromagnetic field energy density:

(10.4)

Thus, the velocity of electromagnetic field is as follows:

(10.5)

Thus:

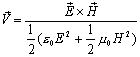(10.6)

As we know:

Thus:

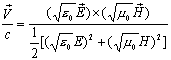(10.7)

Equation (10.7) is the electromagnetic field velocity equation.

From the equation (10.7), we found out that the value of velocity is always less than the speed of light c, when and only when both of the follows two conditions are satisfied, the velocity will equal to speed of light, which are:

(10.8)

And

(10.9)

Thus:

(10.10)

Combine the equations (4.2) and (5.2) into (10.7), then we can get the velocity of electromagnetic field inside the electron as follows:

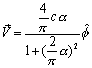(10.11)

In which is the azimuthal angle.

From the above equation, we find out that inside of the electron, the velocity is around the azimuthal direction, and that the speed inside of the electron has constant value.

As we know:

Thus:

(10.12)

Reference

What is the Velocity of the Electromagnetic Field?

Wilhelm Fushchych

Journal of Nonlinear Mathematical Physics 1998, V.5, N 2, 159–161.

A note on magnetic monopoles and the one dimensional MHD Riemann problem
Paul J. Dellar
Journal of Computational Physics 172, 392–398 (2001)

Conservation of Circulation in Magnetohydrodynamics
Jacob D. Bekenstein, Asaf Oron
Phys.Rev. E62 (2000) 5594-5602

Relativistic electrons on a rotating spherical magnetic dipole: surface orbitals

James M. Gelb, Kaundinya S. Gopinath, Dallas C. Kennedy

Int.J.Mod.Phys. D8 (1999) 229

Hamilton's principle for electromagnetic fluids
H. A. Haus and P. L. Penfield
Phys. Fluids 9, 1195-1204, Feb. 1966.

Towards an Exact Mechanical Analogy of Particles and Fields

Valery P.Dmitriyev

Nuov.Cim. 111A, N5, pp.501-511 (1998)

Mechanical analogies for the Lorentz gauge, particles and antiparticles

Valery P. Dmitriyev

Apeiron, vol. 7, no 3-4, pp. 173-183 (2000)

Spinning magnets and Jehle’s model of the electron
D.F. Bartlett et al
Physical Review D, 16 (1977).

Spinning magnets and relativity. Jehle vs. Bartlett
Guala-Valverde
Physica Scripta, The Royal Swedish Academy of Sciences, 66, (2002).