Chapter 17 --- The electromagnetic model of the hydrogen atom

Chapter
17

The electromagnetic model
of the hydrogen atom

               Despite the hydrogen atom’s overall neutrality, hydrogen does have an internal distribution of electric charge.

As we know that the simplest hydrogen atom consists of one proton and one electron, the hydrogen atom as total has zero electric charge. Combine both electron charge distribution and proton charge distribution together, then we can get the hydrogen atom’s electric charge distribution as follows:

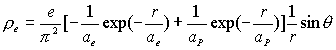(17.1)

Hydrogen atom magnetic charge density distribution equation:

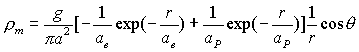(17.2)

Hydrogen atom electric charge distribution equation:

(17.3)

Hydrogen atom magnetic charge distribution equation:

(17.4)

Hydrogen atom electric field equation:

(17.5)

Hydrogen atom magnetic field equation:

(17.6)

Base on these equation, we can get hydrogen magnetic field energy:

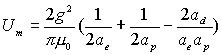(17.7)

In which

(17.8)

Thus:

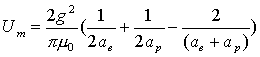(17.9)

Thus:

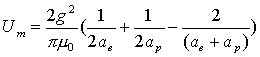(17.10)

Thus:

(17.11)

The hydrogen electric field energy is:

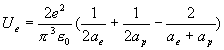(17.12)

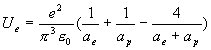(17.13)

Thus, the hydrogen atom’s electromagnetic energy is:

(17.14)

Thus:

(17.15)

As we know

(17.16)

Thus:

(17.17)

Thus:

(17.18)

As we know:

(17.19)

(17.20)

Thus:

(17.21)

Thus, the momentum density for hydrogen is:

(17.22)

The energy density for hydrogen is:

(17.23)

(17.24)

Thus, the velocity of a hydrogen atom is:

(17.25)

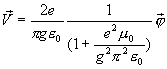(17.26)

Thus:

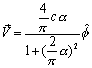(17.27)

We find out that inside the hydrogen atom, the velocity is the same as for the electron, which has a constant speed value.

As we know the field angular momentum density is:

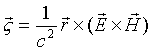(17.28)

Thus, the hydrogen atom field angular momentum is as follows:

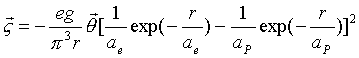(17.29)

Then, integrating equation (17.28), we can get the field angular momentum:

(17.30)

(17.31)

For the cylindrical coordinates (, , z), which has the following relationship with the spherical coordinate (r, , ):

We can separate the angular momentum density into z component and component,

The z component of angular momentum density is:

(17.32)

Thecomponent of angular momentum density is:

(17.33)

As we know, the volume element is:

For the component of angular momentum density, because

(17.34)

Thus, we can get the component of angular momentum:

(17.35)

For the z component of electron angular momentum, we have:

(17.36)

Thus:

(17.37)

Thus:

(17.38)

Thus:

(17.39)

When , thus the z component of angular momentum is:

(17.40)

When thus:

(17.41)

In which

(17.42)

Thus:

(17.43)

As we know eg= h

Thus:

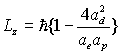(17.44)

Thus:

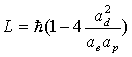(17.45)

Thus:

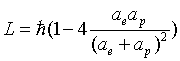(17.46)

Thus:

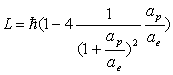(17.47)

As we know

(17.48)

Thus:

(17.49)

Based on the equations (17.3) and (17.4), we can get the ratio of magnetic charge and electric charge inside the hydrogen atom:

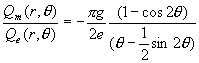(17.50)

For the whole north pole area which is within

Thus:

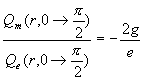(17.51)

For the whole south pole area which is within

Thus:

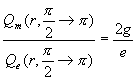(17.52)