Chapter
18

The electromagnetic model
of the neutron
 

 

The neutron as a whole has zero electric charge and zero magnetic charge, but the neutron still has an intrinsic electric field and magnetic field.

 

The neutron in total has zero electric charge and magnetic charge, but similar to the electron and proton, the neutron still has half spin.

Let us compare the neutron and hydrogen atoms, both as a total have zero electric charge and zero magnetic charge, and both have intrinsic electric field and magnetic field. The major difference is the neutron alone has half spin.

 

Let us assume that a neutron has a similar internal structure to a hydrogen atom. Then we can make an assumption that the neutron’s electric and magnetic charge distribution equation is as follows:

 

                                                        (18.1)

 

The neutron’s magnetic charge density distribution equation is as follows:

 

                                                (18.2)

 

The neutron as whole has no electric charge, but has half spin. Here is the model for the neutron, which has a similar electromagnetic structure as a hydrogen atom. The difference is that the hydrogen atom has spin 1, but the neutron has half spin.

 

Similar to the hydrogen atom spin formula, we can get the neutron’s angular momentum as follows:

 

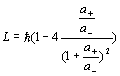                                                                                                    (18.3)

 

As we know neutrons have half spin, so:

 

                                                                                                                      (18.4)

 

Let us make an assumption that

 

 

Thus:


                                                                                                           (18.5)

 

Thus:

 

                                                                                                         (18.6)

 

We can get the neutron’s magnetic field energy as follows:

 

                                                                          (18.7)

 
Thus:
 

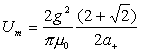                                                                                               (18.8)

 

Thus:
 

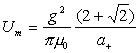                                                                                               (18.9)

 

Thus:

 

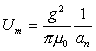                                                                                                        (18.10)

 

In which

 

                                                                                                      (18.11)

 

Thus:

 

                                                                                                    (18.12)

 

Therefore, we can get the neutron’s electric field energy as follows:

 

                                                                        (18.13)

 
Thus:
 

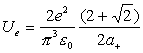                                                                                            (18.14)

 

Thus:
 

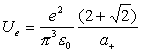                                                                                             (18.15)

 

Thus:

 

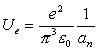                                                                                                       (18.16)

 

As we know, the electromagnetic field energy is:

 

                                                                                                           (18.17)

 

Thus:

 

                                                                                                  (18.18)

 

Thus:

 

                                                                                                                (18.19)

 

 is the neutron mass, thus:

 

                                                                                             (18.20)

 

Thus:

 

                                                                                              (18.21)

 

Thus:

 

                                                                                                      (18.22)

 

                                                                                            (18.23)

 

As we know,

 

                                                                                                         (18.24)

 

Thus:

 

                                                                (18.25)

 

Thus:

 

                                                                             (18.26)

 

Compare this with the electron formula:

 

                                                                                             (18.27)

 

Thus:

 

                                                                                              (18.28)

 

As we know,

 

                                                                                                           (18.29)

 

Thus:

 

                                                                                                    (18.30)

 

Thus, we get the relationship between the electron mass, neutron mass and their radius relationship:

 

                                                                                                (18.31)

 

                                                                                                   (18.32)

 

 


What is the electron spin?
ISBN 0-9743974-9-0
Copyright © 2003
Gengyun Li
All rights reserved
http://www.electronspin.org