Chapter
23

The hydrogen atom electric charge density distribution equation is:

(23.1)

Hydrogen atom magnetic charge density distribution equation is:

(23.2)

The hydrogen atom electromagnetic field equation as follows:

(23.3)

(23.4)

As we know, the hydrogen atom spectrum in vacuum has following format:

(23.5)

In which is called the Rydberg constant.

The hydrogen atom spectrum is the electromagnetic field wave energy spectrum; the atom spectrum is the result of the electromagnetic field standing wave, which includes both the electric field standing wave and magnetic field standing wave.

According the equation (17.51) and (17.52), we find out that the ratio of the magnetic charge and electric charge within both the north pole and south pole of a hydrogen atom have the same value but opposite sign.

Similar to the electron, let us assume the hydrogen atom’s characteristic impedance is the ratio of magnetic charge and electric charge for both north pole and south pole. Thus we can derive the hydrogen atom’s electromagnetic characteristic impedance as follows:

(23.6)

Outside the hydrogen atom is the vacuum. The vacuum impedance is:

. (23.7)

As we know, the velocity has an inverse relationship with impedance, so the wave velocity inside the hydrogen atom has the following relation with the speed of light.

(23.8)

Then we can get:

(23.9)

The inside of the hydrogen atom has constant impedance and wave velocity. Outside the hydrogen atom, exists a vacuum that has light speed as its wave velocity.

Inside of the hydrogen atom, there are both outgoing and incoming waves along the radial direction, which form a standing wave.

Let’s introduce a new function which we can temporally call the zeta-exponential function [C] as follows:

(23.10)

For m =1 thus:

(23.11)

In which

(23.12)

The value of is always larger than 1, with the increase of the integer n, the value becomes more and more close to the number 1.

As we know, the spherical wave equation [D] is:

(23.13)

We can see both the following functions are the solution of the spherical wave equation [D]:

(23.14)

And

(23.15)

The first solution is a kind of outgoing wave.

The second solution is a kind of incoming wave.

Let us make an assumption that the hydrogen atom electric field with the stationary wave function is as follows:

(23.16)

The hydrogen atom magnetic field equation with the stationary wave is as follows:

(23.17)

In which:

(23.18)

And

(23.19)

The B is the positive constant.

Let us define the constant angle as follows:

(23.20)

Thus:

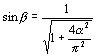(23.21)

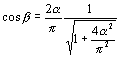(23.22)

As we know the electron’s electric field energy is:

(23.23)

Thus:

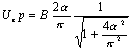(23.24)

Thus:

(23.25)

As we know, the electron magnetic field energy is:

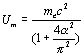(23.26)

Thus:

(23.27)

(23.28)

Thus:

(23.29)

(23.30)

Thus:

(23.31)

(23.32)

(23.33)

Let us define the function f(r) as:

(23.34)

Thus:

(23.35)

(23.36)

The free electron electric field total energy is:

(23.37)

As we know, the electric field energy density is:

(23.38)

Thus:

(23.39)

(23.40)

                                                         (23.41)

(23.42)

(23.43)

(23.44)

The free electron magnetic field energy is:

(23.45)

As we know, the magnetic field energy density is:

(23.46)

Thus:

(23.47)

(23.48)

(23.49)

(23.50)

As we know the electromagnetic field energy density is as follows:

(23.51)

Thus:

(23.52)

From here we can see that the hydrogen atom’s electromagnetic energy spectrum frequency has the following format:

(23.53)

As we already know, the hydrogen atom’s wave velocity is as follows:

(23.54)

Thus:

(23.55)

For the electromagnetic field wave in a vacuum, the wavelength is as follows:

(23.56)

As we know from (9.15), we have:

(23.57)

Thus:

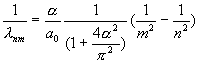(23.58)

Compared with the hydrogen atom spectrum formula (23.5), we can get:

(23.59)

Then:

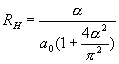(23.60)

Reference

Nonlinear Standing and Rotating Waves on the Sphere
C. Gugg, T.J. Healey, S. Maier-Paape & H. Kielhöfer
J. Differential Equations, vol. 166, (2000), p. 402.

Quantum Spin Chains and Riemann Zeta Function with Odd Arguments
H.E. Boos, V.E. Korepin
J.Phys. A34 (2001) 5311-5316

The Phase of the Riemann Zeta Function and the Inverted Harmonic Oscillator
R.K. Bhaduri,Avinash Khare, J. Law
Phys.Rev. E52 (1995) 486

Path Integrals and Voronin's Theorem on the Universality of the Riemann Zeta Function
Khalil M. Bitar
Nucl. Phys. Proc. Suppl. 26 (1992) 656

Quantum Correlations and Number Theory
H. E. Boos, V. E. Korepin, Y. Nishiyama, M. Shiroishi
J.Phys. A35 (2002) 4443-4452

Free nonlinear vibrations for a class of two-dimensional plate equations: standing and discrete-rotating waves
T. Healey and H. Kielhofer
Nonlinear Anal. 29 (1997), 501-531.

Use of Harmonic Inversion Techniques in Semiclassical Quantization and Analysis of Quantum Spectra
J. Main
Journal-ref: Phys. Rep., 316 (1999) 233-338

Phase of the Riemann zeta function and the inverted harmonic oscillator

R. K. Bhaduri, A. Khare, and J. Law

Phys. Rev. E, 52 (1995), pp. 486-491

Lorentz-invariant hamiltonian and Riemann hypothesis

S. Okubo

J. Phys. A., 31 (1998), pp.1049-1057

The Riemann Zeros and Eigenvalue Asymptotics

M. V. Berry, J. P. Keating

SIAM Review, Volume 41, Number 2 pp. 236-266