|
Chapter |
As
we know, the electromagnetic field has the properties of energy, momentum and
angular momentum. The electromagnetic field momentum density is:
(6.1)
Based upon the electromagnetic field momentum, and then we can define the field angular momentum density as follows:
(6.2)
Thus:
(6.3)
Then
integrating equation (6.3), we can get the field angular momentum:
(6.4)
Combine
the equation (4.2) and (5.2) into equation (6.3),
Thus:
(6.5)
For the cylindrical
coordinate (
, 
, z), which has the follows relationship with the spherical
coordinate (r, 
, 
):
We can separate the angular momentum density into
the z component and 
component,
The
z component of angular momentum density is:
(6.6)
The
component of angular momentum density is:
(6.7)
As
we know the volume element is:
For
the 
component of angular momentum
density, because
(6.8)
Thus we can get
the 
component of angular momentum:
For
the z component of electron angular momentum, we have
(6.9)
Thus:
(6.10)
(6.11)
Therefore:
(6.12)
The
equation (6.12) is the angular momentum distribution equation of an electron.
When 
, the z component of angular momentum is:
(6.13)
The
equation (6.13) is the angular momentum within the sphere of radius r of
an electron.
The
angular momentum distribution is a kind of cumulative gamma distribution in
mathematics [B]
When 
thus:
(6.14)
The above angular
momentum is the electron’s electromagnetic field angular momentum in total.
What is the electron spin? As we know, the electron spin is the electron intrinsic angular momentum. Let us make an assumption that electron spin is the electromagnetic field angular momentum, which also means that the electron spin is of purely electromagnetic origin.
Thus:
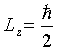(6.15)
Combine (6.14) and
(6.15), thus:
(6.16)
From
equation (6.16), we found out that the multiple of electric charge unit ‘e’ and
magnetic charge unit ‘g’ equal the Planck’s constant ‘h’.
Then, we can also calculate
the ratio of magnetic charge ‘g’ and electric charge ‘e’ as follows:
(6.17)
Thus:
(6.18)
So:
(6.19)
Thus:
(6.20)
As we know, the
vacuum impedance is:
(6.21)
So we can see the ratio of magnetic charge unit ‘g’ and electric charge unit ‘e’ has the unit of impedance.
Reference
Electromagnetic
field angular momentum in condensed matter systems
Douglas Singleton, Jerzy Dryzek
Phys. Rev. B, 62, 13070 (2000)
Electromagnetic
angular momentum and quantum mechanics
D. Singleton
Am. J. Phys. 66, 697 (1998)
A
derivation of the classical monopole energy loss from angular momentum conservation
J. S. Trefil
Am. J. Phys. 51, 1113 (1983)
N. Gauthier
Am. J. Phys. 70, 1034 (2002)
Field
angular momentum in atomic sized systems
Jerzy Dryzek , Douglas Singleton
Am. J. Phys. 67, 930 (1999)
Electromagnetic
momentum density and the Poynting vector in static fields
Francis S. Johnson, Bruce L. Cragin, and R. Richard Hodges
Am. J. Phys. 62, 33 (1994)
David J. Griffiths
Am. J. Phys. 60, 979 (1992)
Peter H. Ceperley
Am. J. Phys. 60, 938 (1992)
V. Hnizdo
Am. J. Phys. 60, 242 (1992)
Electromagnetic
angular momentum for a rotating charged shell
Antonio S. de Castro
Am. J. Phys. 59, 180 (1991)
Angular
momentum of a charge–monopole pair
K. R. Brownstein
Am. J. Phys. 57, 420 (1989)
Angular
momentum in the field of an electron
Jack Higbie
Am. J. Phys. 56, 378 (1988)
Angular
momentum in static electric and magnetic fields: A simple case
H. S. T. Driver
Am. J. Phys. 55, 755 (1987)
Hans C. Ohanian
Am. J. Phys. 54, 500 (1986)
Electromagnetic
angular momentum
Robert H. Romer
Am. J. Phys. 53, 15 (1985)
Field
angular momentum of an electric charge interacting with a magnetic dipole
A. C. Lawson
Am. J. Phys. 50, 946 (1982)
Angular
momentum of a static electromagnetic field
E. Corinaldesi
Am. J. Phys. 48, 83 (1980)
The
Law of Conservation of Angular Momentum
Ph. M. Kanarev
Journal of Theoretics Vol.4-4
Ph. M. Kanarev
APEIRON Vol. 7 Nr.
3-4, July-October, 2000
|
What
is the electron spin?
ISBN 0-9743974-9-0 Copyright © 2003 Gengyun Li All rights reserved http://www.electronspin.org |